Math - 3D and Perspective
In our last blog post we used matrices to translate, rotate and scale vectors, but so far only in 2D.
Transforming vectors in 3D is pretty much the same thing. The only difference is that we cannot directly plot those vectors out on the screen since each vector will come in a triplet of {x,y,z} and the screen only consists of {x,y}.
We could just ignore the Z-coordinate, but that would look weird!
To get it to look right we need to apply perspective. Perspective means that an object that is further away from our eye will appear smaller than an object that is closer!
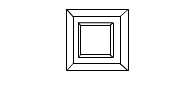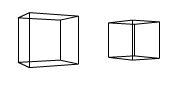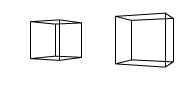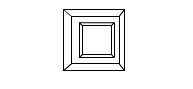
Applying perspective to 3D-points is something I’ve been able to do for a long time, but now we’re working with matrices, and of course there is something called a perspective projection matrix!
Another great resource I found on the subject is scratchpixel.com, here on Perspective Matrix Projection.
In the past when I’ve been playing with 3D, I’ve used trigonometry for all transformations. It works, but has several drawbacks!
- More computation heavy! Needs to do Sine and Cosine lookup for each point!
- Much more complex to nest parent/child-relationship!!
- Viewing from a camera… I don’t think so!

Using matrices is superior by far. The image below is just a couple of matrices combined, using vectors forming a cube and a pyramid. This would not have been possible using my old 2006 methods!
If you want to read up on this too, then check out:
Math for game developers youtube channel And http://www.scratchapixel.com/index.php?nocategory
