Math - Matrices and Vectors
After my Shader Week I decided to try to re-wake the math part of my brain that feels like it has numbed of a bit in recent years of Android app development. I have actually been doing this for several weeks now, but have not had anything to show until now.
So I started reading up on Linear Algebra, and is currently writing my own custom implementation of Vector and Matrix-classes from scratch in Haxe. And it’s super interesting!
Rotation Matrix
If you have a 2x2 matrix you can put an up-vector in the first column and a right-vector in the second column. When multiplying a vector with this rotation-matrix it will transform the vector into that coordinate space! If you rotate the up and right-vector clockwise each frame you get a rotation matrix!
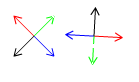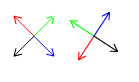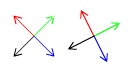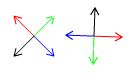
In this first image I multiply four 2d-vectors through a rotation matrix. The unmodified vectors are shown to the left.
TRS Matrix (Translate Rotate Scale)
Another interesting thing with matrices is that you can combine them! If you have one matrix for translation, one for rotation and one matrix for scaling, you can get a single matrix containing all those values by multiplying them! Just remember to multiply them in the correct order!

Parenting
If you have a TRS-matrix named M1, and another TRS-matrix named M2, you can move the transformation of M2 into the local coordinate space of M1 by multiplying M2 with M1! By doing this M2 will be “parented” to M1! It’s so simple!
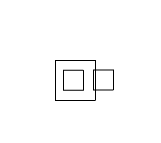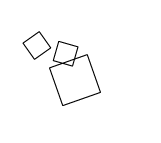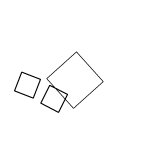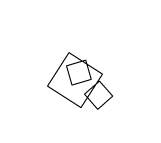
The big square is rotating and the second, smaller square is parented to the big one, therefore inheriting its rotation. Same with the third square (it inherits both the rotation and scale of it’s parent before applying its own rotation).
The vectors (points) for all three squares are just a single unmodified array. All the transformations are done though a single matrix multiplication (for each point).
I will keep working through the math, so expect more posts on this. In the mean time, these two youtube playlists are really great resources:
