Separating Axis Theorem - for idiots

The Original Problem:

I need to know if two rectangles are overlapping.

• Rectangle is the only shape I need to check
• The rectangles are NOT rotated
• The rectangles can be of different sizes

There are several possible ways to solve this.

• Check if any of the corner points is inside the other, since point-vs-rectangle-test is so easy to write. But doesn’t work if rectangles has different sizes.
• Clip them and check if the area is empty or negative
• Use the Separating Axis Theorem

The last option is what we want to do in this case.

Separating Axis Theorem (SAT) basics…

Note: This is not an extensive explanation of the SAT (there are a ton of resources on it, like this: https://www.youtube.com/watch?v=Aqj1Z1vgE6I&), also - this is a simplified version of SAT as we only use axis aligned (non rotated) rectangular shapes

We could say that if it is possible to draw a straight line between two shapes, then it’s impossible for them to touch. Look at the following image, where you can draw a straight horisontal line in the first, a straight vertical in the second, but no line through the last.

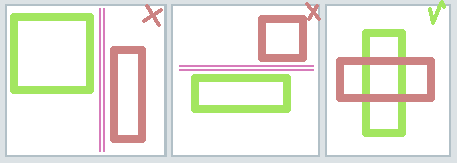
SAT works by

• Take each side of the rectangles and turn them into a line {min, max}
• Check if any of the lines overlap each other
• If they do NOT overlap, then we know they don’t overlap and can do a possibly early exit
• If they DO overlap, continue
• The rectangles DO overlap if the line segments overlaps on both axis

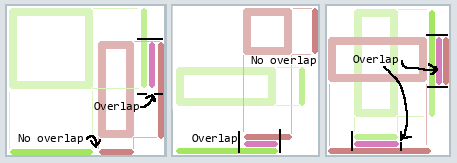
So now we need to check if two line segments overlap or not.

How to check if two line segments overlap (my REAL problem)

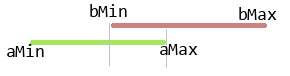Here’s how the algorithm looks in full:

bool overlap = b.xMax > a.xMin && b.xMin < a.xMax && b.yMax > a.yMin && b.yMin < a.yMax;

And now to my real problem. The algorithm is easy enough to find with google or AI, but what does all these checks actually do? Why can’t I wrap my head around it? Why don’t I remember it directly in my mind as I do with point-in-rectangle or pythagoras or trigonometry?

Let’s break it down so even my poor brain understand this algorithm

Step 1 - are we too far to the left?

We know that if the two lines do not overlap, then the rectangles do not overlap.

One way for these lines to NOT overlap is if B is to the left of A.

But we’re checking if we ARE overlapping, so we need to know that B is NOT to the left of A - which we can see is pretty trivial:

bool notTooFarToTheLeft = bMax > aMin;

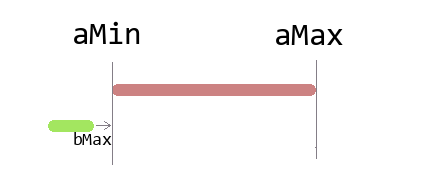
Step 2 - are we too far to the right?

Now we know we are not too far to the left, but we can still be too far to the right!

bool notTooFarToTheRight = bMin < aMax;

Step 3: combine

Now we know we are inside if we are not too far to the left AND not too far to the right:

bool lineOverlaps = notTooFarToTheLeft && notTooFarToTheRight;

or…

bool lineOverlaps = bMax > aMin && bMin < aMax;

Now all we need to do is combine for both axis:

bool overlap = 
     b.xMax > a.xMin && b.xMin < a.xMax && 
     b.yMax > a.yMin && b.yMin < a.yMax;

A note about inclusivity/exclusivity

Inclusive/exclusive is the next thing that may cause confusion. Exactly what does the values min and max stand for?

Normally, I prefer rectangles to be defined as:

struct Rectangle { int x, y, w, h; }, and xMin = rect.x and xMax = rect.x + rect.w;

Let’s say that I have a rectangle where x = 0 and w = 3, that would give xMin = 0 and xMax=3 In asciibrain I render a rectangle in a terminal window with a simple for-loop:

for (int x = min; x < max; ++x)

This WILL draw at xMin (inclusive), but it will NOT draw xMax (exclusive)

This is important for the equality-signs! Let’s do a sanity check. Look at step 1 again, and let’s give example values:

aMin = 10 and bMax = 10, i.e. B is to the left, but they are “touching” edge to edge (because B does not actually DRAW at x=10).

bool notTooFarToTheLeft = 10 < 10; // false Great! This returns false as they are NOT overlapping!

Let’s check the other side too, with a new B line and check step 2:

aMax = 20 and bMin = 20. This time B is to the right, but touch edge-to-edge.

bool notTooFarToTheRight = 20 > 20; // false Great! Also not touching!

Note that the two checks uses different B line examples. If we have a line with {min = 20, max = 10 } then we’re checking an inverted line, which we ofc don’t do

Now we are good to go! Hopefully this makes more sense. I’ve been trying to wrangle my brain around this line-line formula for way too long, so now I write it down for myself. But I finally get this by now!